영상 워핑과 모핑

영상 워핑 (Warping)

픽셀의 위치를 변환하여 영상을 왜곡시키는 것을 영상 워핑이라고 합니다. 영상 워핑은 기하학적 처리 중 하나로, 임의의 기하학적 변환에 의해 화소들의 위치를 변경하는 처리를 말합니다.

각 픽셀 별로 이동 정도가 다르다는 점에서 기본 기하학적 처리(회전, 확대, 축소 등)와 차이가 있습니다.
영상 워핑은 픽셀의 위치를 변환하는 것이기 때문에, 영상의 전체적인 구조를 유지하면서 특정 부분을 왜곡시키는 데에 사용됩니다.

제어선, 제어점, 그물망, 다각형 등 다양한 대응관계 기술을 사용하여 영상을 왜곡시킬 수 있습니다.

점 대응 매핑 (Point Correspondence Mapping)

영상 워핑을 위해서는 원본 영상과 변환된 영상 사이의 점 대응 관계를 알아야 합니다.
점 대응 관계를 알기 위해서는 점 대응 매핑이 필요합니다. 점 대응 매핑은 원본 영상과 변환된 영상 사이의 대응 관계를 정의하는 것입니다.

점 대응 매핑은 제어점을 이용하여 대응 관계를 정의합니다. 제어점은 원본 영상과 변환된 영상 사이의 대응 관계를 정의하는 점입니다.
제어점을 이용하여 점 대응 관계를 정의하면, 제어점을 이용하여 영상을 왜곡시킬 수 있습니다.

Barycentric Coordinate, Thin Plate Spline, Radial Basis Function, Delaunay Triangulation 등 다양한 점 대응 매핑 기술이 있습니다.

박판 스플라인 워핑 (Thin Plate Spline)

Thin Plate Spline은 점 대응 관계를 정의하는 방법 중 하나입니다.
대응점들의 변형을 기준으로 다른 점들의 변형을 결정하는 전역적인 점 대응 관계를 정의합니다.
Thin Plate Spline은 최소 에너지를 갖는 플레이트를 이용하여 점 대응 관계를 정의합니다.

제어선을 이용한 워핑

출력 영상의 픽셀 $V$에 대응되는 입력 영상의 픽셀 $V’$를 찾아서 픽셀값을 복사하는 방법입니다.
여기서 제어선은 입력 영상과 출력 영상 사이에서 특징들을 서로 연결하는 역할을 합니다.

아래의 그림과 같이 화소와 제어선 사이의 수직 교차점을 구하고,

1. 화소($V$)와 수직 교차점($C$) 사이의 변위 정보와
2. 제어선 내에서 수직 교차점의 위치 정보

두 가지를 활용하여 워핑 과정에서 출력 영상의 픽셀에 해당되는 입력 영상의 픽셀을 찾아가는 역방향 사상 방법을 수행합니다.

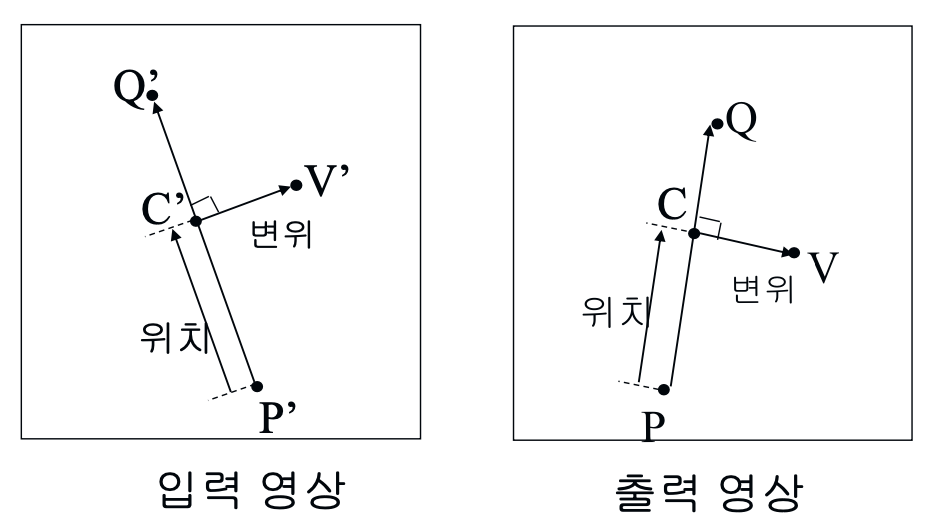
각각의 정보를 구하는 수식은 다음과 같습니다.

• 위치 정보 : $u = \frac{(V - P) \cdot (Q - P)}{|Q - P|^2}$
• 변위 정보 : $h = \frac{(V - P) \times Perpendicular(Q - P)}{|Q - P|}$
• 위치 정보와 변위 정보를 이용하여 입력 영상의 픽셀을 찾습니다. \(V' = P' + u \cdot (Q' - P') + h \cdot \frac{Perpendicular(Q' - P')}{\|Q' - P'\|}\)

$u$는 제어선을 따라서 위치하며, P에서 Q 방향으로 0~1 사이의 값을 가집니다.
$u$는 제어선 바깥에 존재할 수도 있는데, 이 경우에는 $u$가 0보다 작거나 1보다 큰 값을 가집니다.

$h$는 제어선에서의 수직 거리를 나타냅니다. 픽셀이 제어선 위쪽에 위치할 경우 양수, 아래쪽에 위치할 경우 음수를 가집니다.
픽셀이 제어선 위에 위치할 경우 $h$는 0이 됩니다.

위의 그림은 1개의 제어선을 사용한 경우를 보여주고 있습니다.
하지만, 일반적인 모핑에서는 여러 개의 제어선들이 지정되고 연속적으로 적용되어 모핑이 이루어지게 됩니다.

가중치

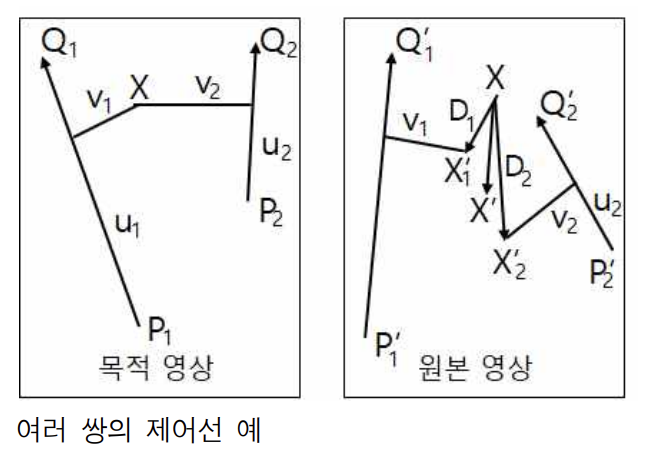
제어선이 여러 개일 때 각 제어선은 영상의 모든 픽셀에 영향을 미치게 됩니다.
픽셀이 여러 개의 제어선에 의해 영향을 받을 때, 각 제어선의 영향력을 결정하기 위해 가중치를 사용합니다.

\[weight = (\frac{length^P}{(a + dist)})^b\]

• $P$는 제어선의 길이가 가중치에 영향을 주는 정도를 결정하는 값으로 0~1 사이의 값을 가집니다.
• $a$는 0으로 나누는 것을 방지하기 위해 사용되는 값으로 매우 작은 값을 가집니다.
• $b$는 제어선의 길이와 거리의 변화에 따라 가중치의 변화 정도를 조절하는 값인데 보통 0.5 ~ 2.0 사이의 값을 사용합니다. 이 값이 커지면 픽셀들은 먼 거리에 있는 제어선들로부터 영향을 적게 받게 됩니다.

픽셀과 제어선의 거리 계산을 위해 $Perpendicular(Q - P)$를 사용합니다. 수직 교착점($C$)이 제어선 내부에 위치할 경우, $dist$는 $h$와 같은 값을 가집니다.
그러나 수직 교착점이 제어선의 외부에 위치할 경우, $dist$는 가장 가까운 제어선의 꼭짓점과의 거리가 됩니다.

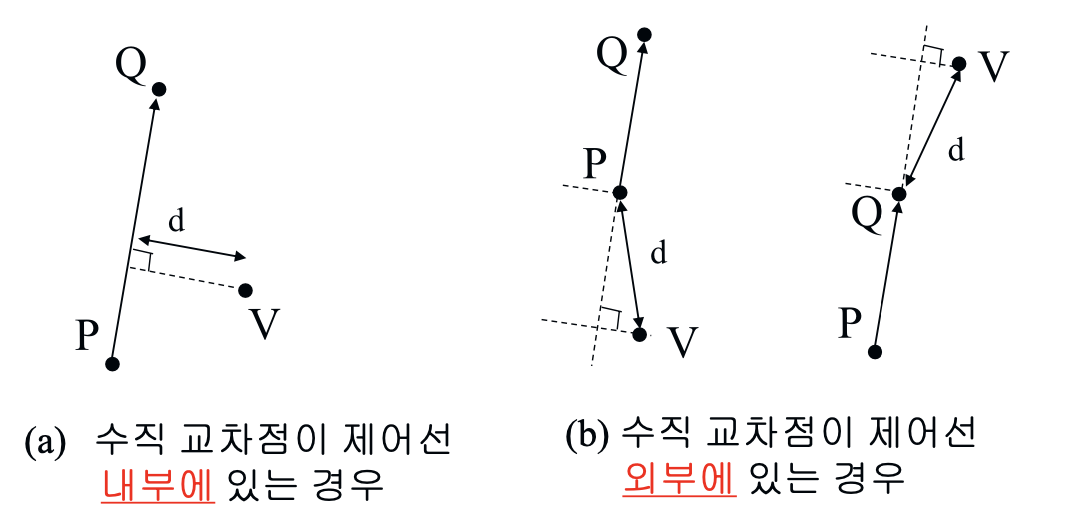
각 제어선에 대하여

1. 출력 영상의 픽셀 $V(x, y)$에 대응되는 입력 영상의 픽셀 $V’(x’, y’)$을 구하고
2. 가중치 $weight$를 구한 다음에는

다음 식과 같이 $V$와 $V’$사이의 변위와 가중치의 곱을 계산하여 $t_x$, $t_y$ 변수에 누적합니다.

\[t_x = t_x + weight \times (x' - x) \\ t_y = t_y + weight \times (y' - y) \\ totalWeight = totalWeight + weight\]

각 제어선에 대해 출력 영상의 픽셀 $V(x, y)$에 대응되는 입력 영상의 픽셀의 변위값을 구하여 이들의 합($t_x$, $t_y$)를 계산한

다음에는 다음 식에 의하여 $V(x, y)$에 대응되는 입력 영상의 픽셀 $V(X, Y)$의 위치를 계산합니다. \(X = x + \frac{t_x}{totalWeight} \\ Y = y + \frac{t_y}{totalWeight}\)

이와 같이 최종적으로 $V(x, y)$에 대응되는 픽셀 $V(X, Y)$를 구한 다음에는 입력 영상의 $V(X, Y)$ 픽셀의 값을 출력 영상의 $V(x, y)$ 픽셀에 복사합니다.

영상 모핑 (Morphing)

두 개의 서로 다른 영상을 서서히 변형시켜 하나의 영상으로 만드는 것을 영상 모핑이라고 합니다.
영상 모핑은 영상 워핑 단계와 영상 합병 단계로 이루어져 있는 기술로, 두 개의 영상 사이의 대응 관계를 정의하여 영상을 서서히 변형시킵니다.

워핑 단계

두 영상을 통해 중간 영상을 생성하기 위해서는 워핑 과정에서 두 개의 영상 간 대응 위치를 정의해야 합니다.
두 입력 영상의 제어선으로부터 보간법을 사용하여 중간 프레임에 대한 제어선을 생성할 수 있습니다.

중간 프레임은 N개 생성될 수 있으며, k번째 중간 프레임에 대한 제어선 계산 식은 다음과 같습니다.

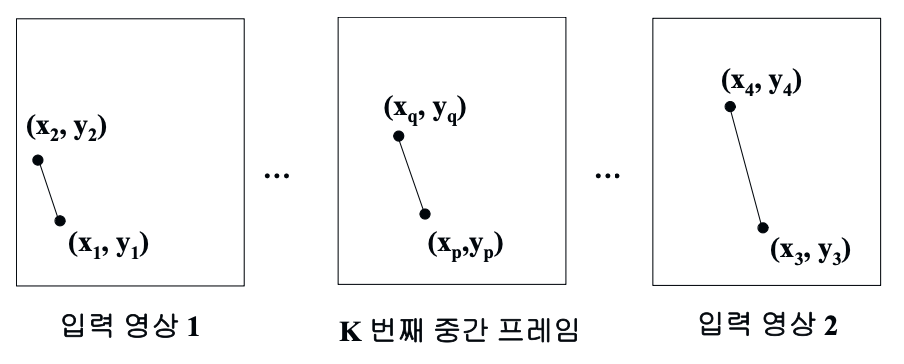
$(k = 1, 2, …, N)$

\(u = \frac{k}{N} \\ x_p = x_1 + u \times (x_3 - x_1) \\ y_p = y_1 + u \times (y_3 - y_1) \\ x_q = x_2 + u \times (x_4 - x_2) \\ y_q = y_2 + u \times (y_4 - y_2)\) k번째 중간 프레임에 대하여 가중치를 계산하고, 해당 가중치를 중간프레임 내에 속한 모든 제어선 계산에 사용합니다.

합병 단계

워핑 단계에서 생성된 중간 프레임들을 합병하여 하나의 영상으로 만드는 단계입니다.
중간 프레임들을 합병하는 방법은 다음과 같습니다.

\(O(x,y) = (1 - u) \times I_1 + u \times I_2\)

• $O$ : 출력 영상
• $I_1$ : 첫 번째 입력 영상으로부터 복사되는 픽셀 값
• $I_2$ : 두 번째 입력 영상으로부터 복사되는 픽셀 값

참고자료

• 제어선을 이용한 워핑 설명
• 영상 워핑
• 영상 워핑과 모핑